Research

My current research aims to promote coastal resilience by investigating efficient shapes of structures on or near the shoreline to sustain extreme wave loads via numerical simulations, experiments, and Bayesian Optimization.

I am also interested in developing differentiable finite element analysis solver to help generic structural optimization in the conceptual design stage of structural and architectural design. For details, please refer to this Github repo: JAX-SSO

For a comprehensive list of my publications, please see my Google Scholar profile. Some of my previous publications are briefly introduced as follows.

Some Previous Work

Gaoyuan Wu, Maria Garlock, Investigating the Effects of Box Girder Bridge Geometry on Solitary Wave Force Using SPH Modeling, Coastal Engineering, January 2024, Volume 187, DOI: 10.1016/j.coastaleng.2023.104430

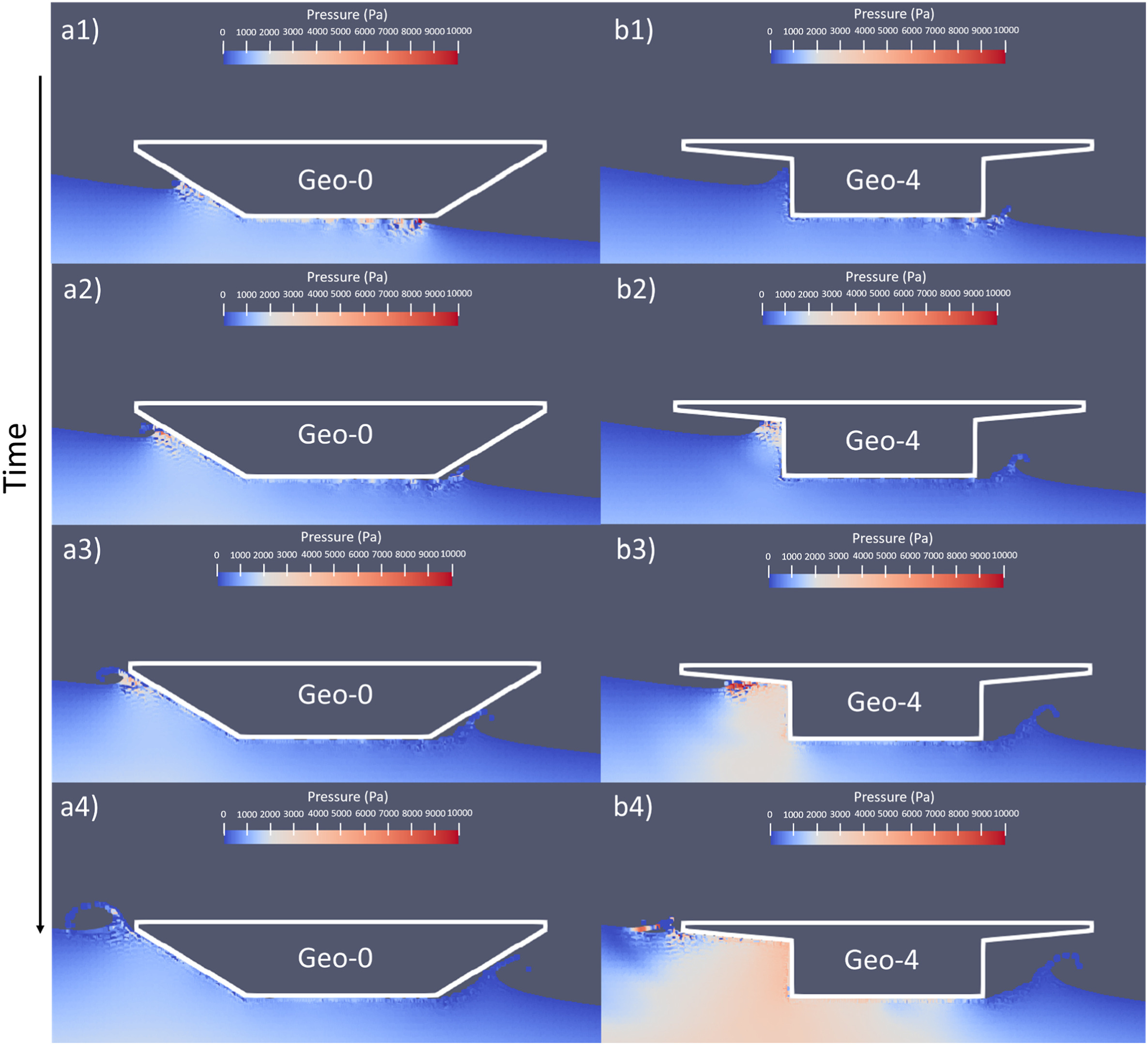
• The potential increase of the intensity and frequency of natural disasters led by climate change indicates higher risks for coastal bridges: they may be lifted off the pier or otherwise fail during hurricane and tsunami strikes because of elevated water and wave forces. This paper investigates various geometries of box girder bridges via smoothed particle hydrodynamics (SPH) modeling, evaluating effective geometric forms and vulnerability. Specifically, we investigate the influence of the angle difference between the web and the top flange, as well as the integration of parapets on wave forces, including the maximum uplift force and the maximum horizontal force. Different wave characteristics and bridge elevations are considered. While both hurricane-induced and tsunami-induced waves would cause damage to coastal box girder bridges, we limit the scope to tsunami-induced waves and thus, solitary waves are employed. The numerical scheme is first validated by existing data in literature and then implemented for a parametric study. It is shown that the angle difference between the web and the top flange plays a significant role in the magnitude of the wave forces, especially when the bridges are elevated and tall waves strike. Moreover, the integration of parapets leads to higher risks for coastal bridges. The results provide insights on effective box girder bridge forms for coastal hazard mitigation, facilitating future research on innovative design of coastal bridges.

Gaoyuan Wu, A framework for structural shape optimization based on automatic differentiation, the adjoint method and accelerated linear algebra, Structural and Multidiscplinary Optimization, June 2023, Volume 66, Page 151, DOI: 10.1007/s00158-023-03601-0

• Shape optimization is of great significance in structural engineering, as an efficient geometry leads to better performance of structures. However, the application of gradient-based shape optimization for structural and architectural design is limited, which is partly due to the difficulty and the complexity in gradient evaluation. In this work, an efficient framework based on automatic differentiation (AD), the adjoint method and accelerated linear algebra (XLA) is proposed to promote the implementation of gradient-based shape optimization. The framework is realized by the implementation of the high-performance computing (HPC) library JAX. We leverage AD for gradient evaluation in the sensitivity analysis stage. Compared to numerical differentiation, AD is more accurate; compared to analytical and symbolic differentiation, AD is more efficient and easier to apply. In addition, the adjoint method is used to reduce the complexity of computation of the sensitivity. The XLA feature is exploited by an efficient programming architecture that we proposed, which can boost gradient evaluation. The proposed framework also supports hardware acceleration such as GPUs. The framework is applied to the form finding of arches and different free-form gridshells: gridshell inspired by Mannheim Multihalle, four-point supported gridshell, and canopy-like structures. Two geometric descriptive methods are used: non-parametric and parametric description via Bézier surface. Non-constrained and constrained shape optimization problems are considered, where the former is solved by gradient descent and the latter is solved by sequential quadratic programming (SQP). Through these examples, the proposed framework is shown to be able to provide structural engineers with a more efficient tool for shape optimization, enabling better design for the built environment.

Gaoyuan Wu, Maria Garlock, and Shengzhe Wang, A decoupled SPH-FEM analysis of hydrodynamic wave pressure on hyperbolic-paraboloid thin-shell coastal armor and corresponding structural response, Engineering Structures, vol. 268, p. 114738, Oct. 2022, doi: 10.1016/j.engstruct.2022.114738

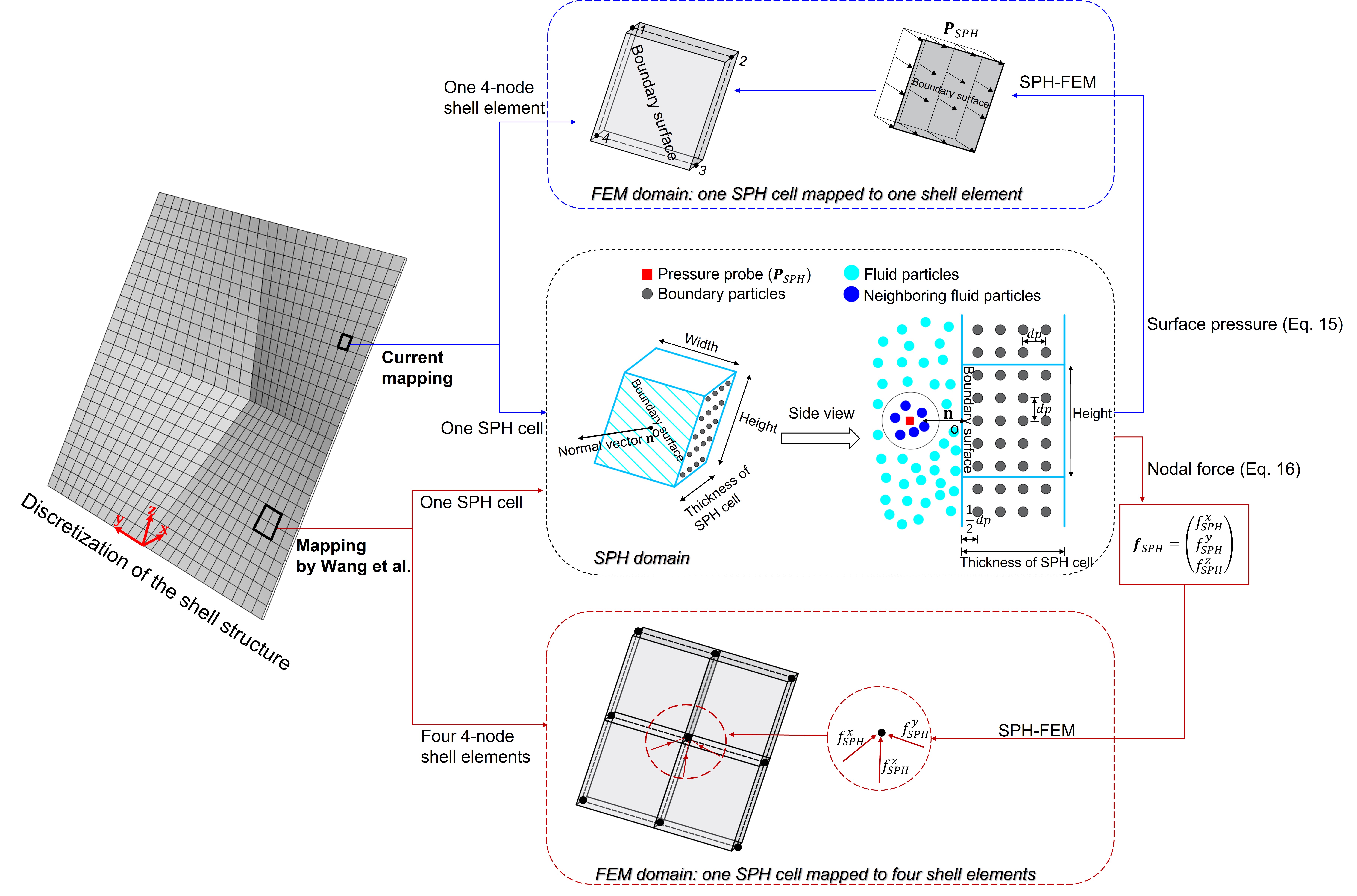
• This work studies the interaction between waves and Kinetic Umbrellas, a newly proposed structural solution for coastal hazard mitigation. A decoupled numerical scheme consisting of Smoothed Particle Hydrodynamics (SPH) and Finite Element Modeling (FEM) is illustrated and implemented to study the wave pressure and corresponding structural response. The results show that hypar thin shells are structurally feasible under surge and wave loadings, which can serve as a sustainable alternative to traditional coastal barriers that are uni-functional and structurally inefficient. The presented framework for studying wave-shell interaction can be generalized for various structural geometries.

Gaoyuan Wu, Rafael Pastrana, Sigrid Adriaenssens, Maria Garlock, A numerical comparison between geometric stiffness- and elastic stiffness-based structural shape optimization for gridshells, Proceedings of IASS Annual Symposia, IASS 2023 Melbourne Symposium: Computational form-finding, pp. 1-13(13) PDF

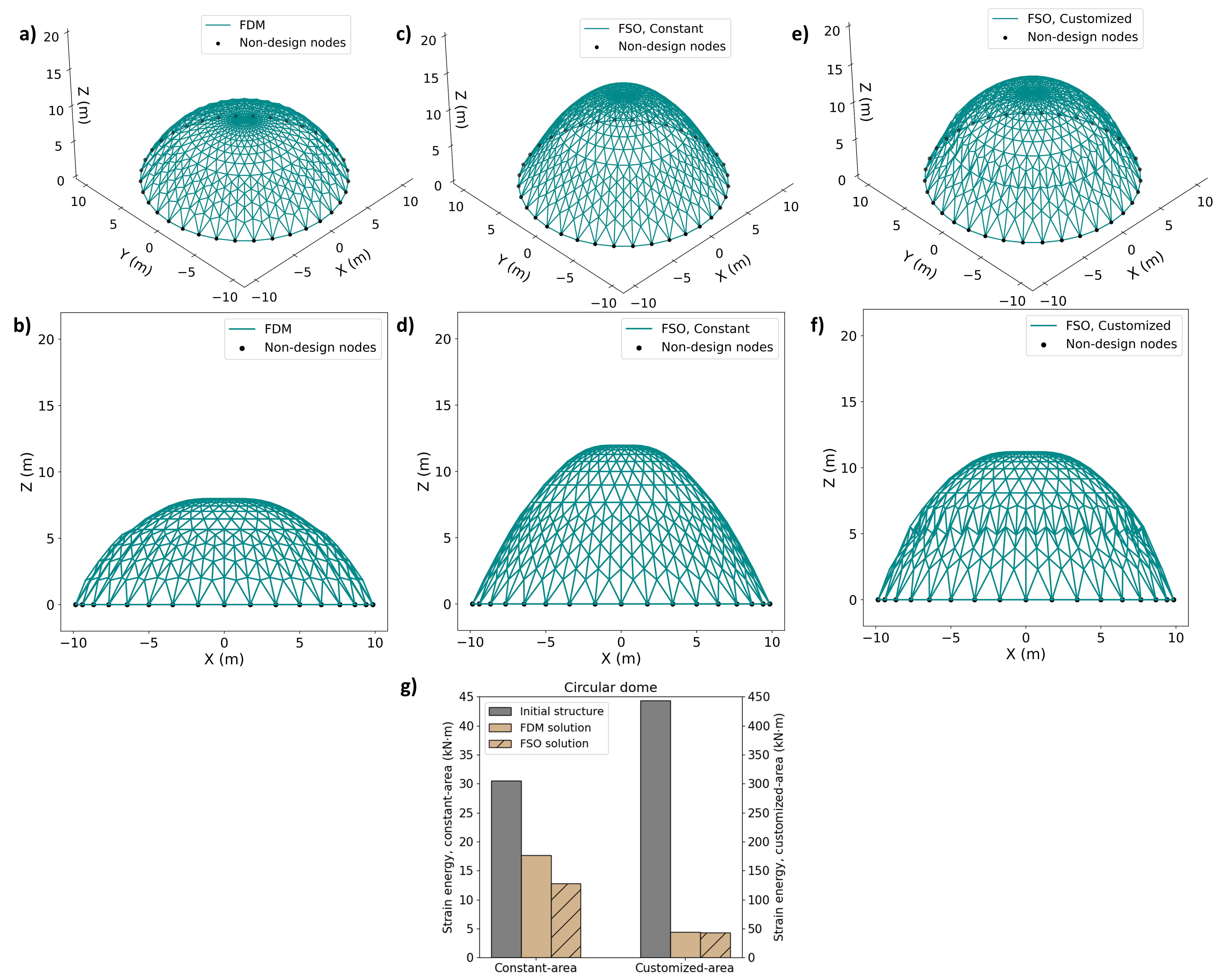
• Gridshells can span long distances efficiently if they have an adequate form. Numerical form-finding methods coupled with optimization algorithms generate such efficient shapes for gridshells based on different stiffness assumptions. These stiffness assumptions may condition the optimality of the generated shape. This paper presents a comparative study between the constrained force density method (FDM) and the finite element analysis (FEA)-based shape optimization (FSO) in the generation of shapes of gridshells that make the optimal use of material as quantified by their strain energy. Three different gridshells with fixed horizontal projection are optimized for minimal strain energy with each form-finding method: a barrel vault, a dome and a gridshell with complex plan view. The optimized gridshell are evaluated after optimization in terms of their strain energy, their maximum height and the incurred optimization runtime. High-performance numerical computing is utilized to execute experiments efficiently and automatic differentiation is leveraged to conveniently obtain the value of the derivatives needed to solve the shape optimization problems herein. The findings of this work provide insights on the strengths and weaknesses of these two form-finding methods, and open new research directions for the practical design of lightweight structures that can mitigate the carbon footprint of the built environment.